#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
@author: Heikki Välisuo
"""
Tämä ohjelma ei käy esimerkiksi tyylikkäästä ohjelmoinnista. Olen selvitellyt pahimpia sotkujani sitä mukaa, kun olen niihin kompastellut. Olen tehnyt sen verran siistiä koodia, että minun on itse tätä melko helppo muutella tarpeen mukaan, mutta tämän lukeminen lienee vaikeaa. Ehkä en vuoden kuluttua itsekään ymmärrä, mitä tässä tapahtuu. Yrittäessäni korjailla omia vanhoja ohjelmiani, olen huomannut, että ohjelmia on helpompi kirjoittaa kuin lukea.
Ohjelmoinnissa on tapana kapseloida yhteen kuuluvia tietoja ja toimintoja olioiksi, joiden sisäisestä elämästä muun ohjelman ei tarvitse tietää mitään. Tyyppiä 'maalari' oleva olio maalaa simuloinnin jokaisella aika-askelella pinnankorkeuksista, virtauksista ja väriaineiden valumisesta kuvan.
Olion voin ajatella maalarin työpajaksi, jolle tarvittaessa lähetetään tiedot järven tilasta ja pyydetään sitä maalaamaan niistä havainnolliset kuvat.
Piirtelyyn käytin matplotlib.pyplot-modulia. Ei ollut helppo oppia sitäkään käyttämään.
import sys
import datetime as tim
import random
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import dfdt_virtaukset as df
import params as par
import saaret as ly
class Cl_Maalari:
# 'figsize=[12.8, 7.2], dpi=100' tuottaa 1280x720 pixelin kuvia,
# joista saa helposti koottua vastaavan resoluution videon
def __init__(self, paint):
plt.ioff()
self.fig, self.taulu = plt.subplots(
1, 2, figsize=[12.8, 7.2],
dpi=100, tight_layout=True)
self.taulu[0].set_aspect('equal')
self.taulu[1].set_aspect('equal')
self.x = np.full(ly.DIM_j, 0.0)
self.y = np.full(ly.DIM_i, 0.0)
for j in range(0, ly.DIM_j):
self.x[j] = par.ds*j
for i in range(0, ly.DIM_i):
self.y[i] = par.ds*i
self.max_speed = 0.0
self.min_paint = np.min(paint)
self.max_paint = np.max(paint)
self.kuvadir = sys.argv[1]
print('kuvadir ', self.kuvadir)
def sys_plot(self, rho, u, v, paint, n):
min_rho, max_rho = np.min(rho), np.max(rho)
# pinnankorkeus. Logaritminen asteikko tuo esiin sekä
# ison konsentraation roiskeet, että diffuusion aiheuttaman
# värien hitaan hiipumisen.
self.taulu[0].pcolormesh(rho, cmap='RdYlGn_r',
norm=colors.SymLogNorm(
linthresh=0.01, base=10))
# virtausnuolet, väri hetkellisen nopeuden mukaan,
# paksuus veden virtauksen mukaan
speed = np.sqrt(u**2 + v**2)
self.max_speed = np.max(speed)
if self.max_speed > 0.01:
q = rho*speed # nesteen virtaus
q_max = np.max(q)
sp_lw = 4.0*q/q_max + 0.1
# clr = (131/255.0, 185/255.0, 0) color=clr)
self.taulu[0].streamplot(self.x, self.y, u, v,
color=speed, cmap='coolwarm',
linewidth=sp_lw)
# väriaineiden konsentraatio
self.taulu[1].pcolormesh(
paint, cmap='RdYlGn',
vmin=par.pnt_cut*self.min_paint,
vmax=par.pnt_cut*self.max_paint)
# norm=colors.SymLogNorm(linthresh=1.0, base=10))
# Näin voi zoomata
# taulu[1].pcolormesh(rho[80:105, 20:60], cmap='plasma_r')
s1 = 'pinnankorkeus {:.4g} -- {:.4g}; '
s2 = ' suurin nopeus: {:.4g}; aika: {:4.1f}'
txt = self.fig.text(0.4, 0.98, (s1+s2).format(
min_rho, max_rho, self.max_speed, n*par.dt,
fontsize='x-large', backgroundcolor='white'))
self.taulu[0].axis('off')
self.taulu[1].axis('off')
# Kuva päivitetään joka simulointiaskelella.
# Ei onnistu ilman pikku pausea
plt.pause(0.01)
# Tallennetaan kuva videon tekemistä varten
figno = '{:05d}'.format(n)
plt.savefig(self.kuvadir + '/taulu_'+figno+'.png', format='png')
# plt.show(block=False)
# Tyhjennetään kuvien sisältö. Muuten uusi kuva tulee vanhan päälle
self.taulu[0].cla()
self.taulu[1].cla()
txt.remove()
Allaolevaan funktiota ei tarvita tässä ohjelmassa, mutta laitoin sen muistutukseksi siitä, että kannattaa olla perillä siitä, miten funktioiden parametrit välittyvät pythonissa.
(Eli siis tein aluksi muutaman vaikeasti jäljitettävän virheen.) Läheskään kaikista webissä olevista selityksistä ei selviä olennainen, mutta allaolevaa funktiota kokeilemalla selviää koko totuus.
def test_swap():
a = np.full((2, 2), 1.0)
b = np.full((2, 2), 2.0)
print(a, '\n', b, '\n\n')
a, b = b, a
print(a, '\n', b, '\n\n')
a = b
print(a, '\n', b, '\n\n')
a[1, 1] = 100.0
print(a, '\n', b, '\n\n')
Sovelsin liiankin paljon paljon yritys-erehdys -menetelmää. Onneksi montaa toimintoa sai testattua piirtämällä kuvan sen tuloksesta.
Alla apufunktiota piirtelyyn. Ohjelmoitu quick-and-dirty copy-paste -menetelmällä
def test_plt1(a, text):
plt.matplotlib.use('qtagg')
plt.ion()
fg, kuva = plt.subplots(1, 1, tight_layout=True)
plt.axis('on')
major_ticks = np.arange(0, ly.DIM_i+1, 10)
minor_ticks = np.arange(0, ly.DIM_i+1, 5)
kuva.set_aspect('equal')
kuva.grid(which='both')
kuva.set_xticks(major_ticks)
kuva.set_xticks(minor_ticks, minor=True)
kuva.set_yticks(major_ticks)
kuva.set_yticks(minor_ticks, minor=True)
kuva.pcolormesh(a, cmap='inferno') # , cmap='winter'
fg.text(0.45, 0.97, text, fontsize='x-large', backgroundcolor='white')
# kuva[0].pcolormesh(a[0:20, 20:60])
# kuva[1].pcolormesh(b[30:90, 60:100])
plt.savefig(text+'.png', format='png')
# plt.show(block=True)
def test_plt(a, kartta, text):
print(text, a.shape)
print(text, kartta.shape)
fg, kuva = plt.subplots(1, 1, tight_layout=True)
plt.axis('on')
major_ticks = np.arange(0, ly.DIM_i+1, 10)
minor_ticks = np.arange(0, ly.DIM_i+1, 5)
kuva.set_aspect('equal')
kuva.grid(which='both')
kuva.set_xticks(major_ticks)
kuva.set_xticks(minor_ticks, minor=True)
kuva.set_yticks(major_ticks)
kuva.set_yticks(minor_ticks, minor=True)
kuva.pcolormesh(a) # , cmap='Spectral_r'
kuva.pcolormesh(kartta, alpha=0.1)
fg.text(0.45, 0.97, text, fontsize='x-large', backgroundcolor='white')
# kuva[0].pcolormesh(a[0:20, 20:60])
# kuva[1].pcolormesh(b[30:90, 60:100])
plt.savefig(text+'.png', format='png')
# plt.show(block=False)
def test_plt2(a, b, kartta, text):
fg, kuva = plt.subplots(1, 1, tight_layout=True)
plt.axis('on')
major_ticks = np.arange(0, ly.DIM_i+1, 10)
minor_ticks = np.arange(0, ly.DIM_i+1, 5)
kuva.set_aspect('equal')
kuva.grid(which='both')
kuva.set_xticks(major_ticks)
kuva.set_xticks(minor_ticks, minor=True)
kuva.set_yticks(major_ticks)
kuva.set_yticks(minor_ticks, minor=True)
x = np.full(ly.DIM_j, 0.0)
y = np.full(ly.DIM_i, 0.0)
for j in range(0, ly.DIM_j):
x[j] = par.ds*j
for i in range(0, ly.DIM_i):
y[i] = par.ds*i
speed = np.sqrt(a**2 + b**2)
max_speed = np.max(speed)
kuva.streamplot(x, y, a, b, linewidth=4.0*speed/max_speed,
color="green") # , cmap='Blues')
kuva.pcolormesh(kartta, alpha=0.1)
fg.text(0.45, 0.97, text, fontsize='x-large', backgroundcolor='white')
plt.savefig(text+'.png', format='png')
# plt.show(block=False)
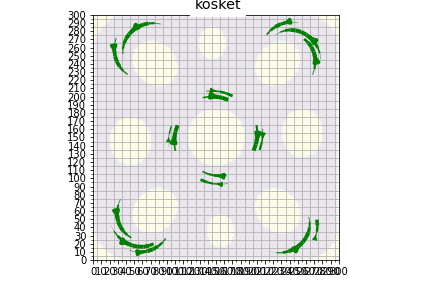
Geometrinen pähkinä:
Koski on ympyrän, jonka keskipiste on (i0, j0) sektorista [kulma0, kulma1] siivu, jonka säde on välillä [r0, r1]. (Mikä mahtaa olla tuollaisen siivun virallinen matemaattinen nimi?)
Koski aiheuttaa ympyrän kehän tangentin suuntaisen voiman F. Koskien aiheuttamat voimat esitetään kahtena NxN taulukkona, joista toisessa x-suuntaiset, toisessa y-suuntaiset voimien komponentit. Tee funktio tätä varten
Lisäksi olisi kiva kallistaa koskea sisäkarteeseen päin, eli lisätä pieni voima, joka osoittaa kohti ympyrän keskipistettä.
(Differentiaaliyhtälöiden numeerisen ratkaisu onnistuu helpommin, kun kaikki on pehmeän pyöreää. Matemaattisesti ilmaisten, kiva, jos funktiot olisivat jatkuvasti derivoituvia. Siksi olisi kiva, jos koski olisi joka suuntaan 'pyöreä'. Jos kosken niskalta voima kasvaa lineaarisesti, koski kääntyy laskuun pyöreästi. ???
Alla on typerä brute-force -ratkaisu. Koska tämä funktio suoritetaan vain kerran jokaisella koskella, koodin tehottomuus ei haittaa, mutta nolottaa kyllä.
def koski(Fe_u, Fe_v, i0, j0, kulma0, kulma1, r0, r1, suunta, tilt, Fe):
rsteps = 200
ksteps = 200
d_kulma = (kulma1 - kulma0)/ksteps
dr = (r1-r0)/rsteps
slope1 = 0.2*ksteps
slope2 = 0.8*ksteps
rslope1 = 0.3*rsteps
rslope2 = 0.7*rsteps
r = r0
for mr in range(0, rsteps):
if mr < rslope1:
rscale = mr/rslope1
elif mr > rslope2:
rscale = (rsteps-mr)/(rsteps-rslope2)
else:
rscale = 1.0
kulma = kulma0
for k in range(0, ksteps):
if k < slope1:
scale = k/slope1
elif k > slope2:
scale = (ksteps-k)/(ksteps-slope2)
else:
scale = 1.0
i = int(math.sin(kulma)*r)
j = int(math.cos(kulma)*r)
F = scale*rscale*Fe
if suunta == 'pos':
Fe_u[i0+i, j0+j], Fe_v[i0+i, j0+j] = \
rotate(F, kulma + np.pi/2.0 + tilt)
else:
Fe_u[i0+i, j0+j], Fe_v[i0+i, j0+j] = \
rotate(F, kulma - np.pi/2.0 - tilt)
kulma += d_kulma
r += dr
Käännetään voimavektori 'kosken' kaarteen suuntaiseksi. Kokeilin satunnaisuuden lisäämistä 'koskiin', mutta tuntui turhalta, joten laitoin kommentiksi
def rotate(R, alfa):
Cu = 1.0 # random.uniform(0.95, 1.05)
Cv = 1.0 # random.uniform(0.95, 1.05)
return Cu*R*np.cos(alfa), Cv*R*np.sin(alfa)
Alla koodissa on 'r1 = 38.0' -tyyppisiä lausekkeita. Yritys-ja-erehdys vaiheessa voi tilapäisesti käyttää tuollaisia häkkeröintejä, mutta jos niitä jää koodiin, koodia on tosi työläs muunnella. Ja muunneltavuus on välttämätöntä.
Ohjelmassani järven koko on NxN ruutua. Mitä suurempi N, sitä tarkempi ratkaisu ja sitä jyrkempiä virtausten mutkia se kykenee ratkaisemaan. Mutta, mitä suurempi N, sitä kauemmin laskenta kestää.
Tätä kirjoittaessani ohjelmani tuottaa taustalla videota varten kuvia noin kuvan sekunnissa. Olisi kiva pienentää N:ää ja kokeilla riittääkö tarkkuus. Vaan mitä kirjoittaa lausekkeen 'r1 = 38.0' tilalle? Miten edes löytäisin kaikki korjaamista tarvitsevat lausekkeet?
'Quick-and-dirty' on dirty, mutta ei quick
Ennen kuin kehitän ohjelmaani pidemmälle, nykyiset tilapäiset häkkäykset pitäisi korjata. Tuota miettiessä projekti alkaa tuntua riittävän valmiilta jo nyt.
def kosket(**kwargs):
Fe_u = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Fe_v = np.full((ly.DIM_i, ly.DIM_j), 0.0)
# ellipsit
i_off = 10
j_off = 10
r0 = 30.0
r1 = 45.0
tilt = 0.2
koski(Fe_u, Fe_v, ly.E_I - i_off, ly.E_J - j_off,
3.0/4.0*math.pi, 7.0/4.0*math.pi,
r0, r1, 'pos', tilt, par.Fe)
koski(Fe_u, Fe_v, ly.E_I - i_off, ly.DIM_j - ly.E_J + j_off,
-3.0/4.0*math.pi, 1.0/4.0*math.pi,
r0, r1, 'pos', tilt, par.Fe)
koski(Fe_u, Fe_v, ly.DIM_i - ly.E_I + i_off, ly.DIM_j - ly.E_J + j_off,
-1.0/4.0*math.pi, 3.0/4.0*math.pi,
r0, r1, 'pos', tilt, par.Fe)
koski(Fe_u, Fe_v, ly.DIM_i - ly.E_I + i_off, ly.E_J - j_off,
1.0/4.0*math.pi, 5.0/4.0*math.pi,
r0, r1, 'pos', tilt, par.Fe)
# keskiympyrä
#
# parametrillä 'vastapyorre' voi valita, 'laskeeko' keskellä
# kiertävä koski myötä- vai vastapäivään
r0 = 45.0
r1 = 60.0
if kwargs['vastapyorre']:
Fey = -par.Fey
tilt = -0.1
else:
Fey = par.Fey
tilt = 0.1
koski(Fe_u, Fe_v, ly.DI_2, ly.DJ_2,
-1.0/8.0*math.pi, 1.0/8.0*math.pi,
r0, r1, 'pos', tilt, Fey)
koski(Fe_u, Fe_v, ly.DI_2, ly.DJ_2,
7.0/8.0*math.pi, 9.0/8.0*math.pi,
r0, r1, 'pos', tilt, Fey)
koski(Fe_u, Fe_v, ly.DI_2, ly.DJ_2,
3.0/8.0*math.pi, 5.0/8.0*math.pi,
r0, r1, 'pos', tilt, Fey)
koski(Fe_u, Fe_v, ly.DI_2, ly.DJ_2,
11.0/8.0*math.pi, 13.0/8.0*math.pi,
r0, r1, 'pos', tilt, Fey)
return Fe_u, Fe_v
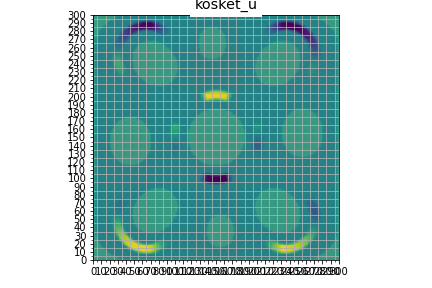
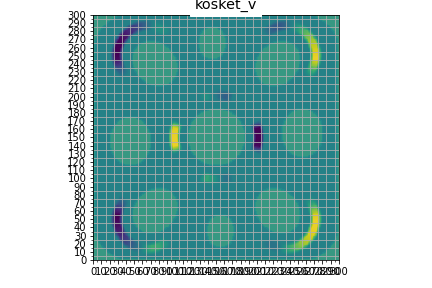
def test_kosket():
a, b = kosket(vastapyorre=True)
n_kartta = test_kartta()
test_plt(a, n_kartta, 'kosket_u')
test_plt(b, n_kartta, 'kosket_v')
test_plt2(a, b, n_kartta, 'kosket')

Koskien voimien ohjelmointia vastaava, mutta helpompi tehtävä: Pyöristä järven kulmat, merkitsemällä R-säteisen ympyrän ulkopuolelle jäävä alue maaksi (= 'saari').
Käydään läpi järven nurkkaan piirretyn R-sivuisen neliön sisään jäävät pisteet ja merkitään maaksi ne, joiden etäisyys järvelle jäävästä neliön sivusta on > R. (Kyllä, jokaisesta geometrisesta ongelmasta kannattaa piirtää kuva)
Olisi tyylikästä ohjelmoida myös 'koski'-funktio tällä periaatteella, mutta en jaksa korjailla.
def kulmatf(kartta, R):
i0 = R
j0 = R
for i in range(0, i0+1):
for j in range(0, j0+1):
if (i0-i)**2 + (j0-j)**2 > R**2:
kartta[i, j] = 'saari'
i0 = R
j0 = ly.DIM_j - R
for i in range(0, i0+1):
for j in range(j0-1, ly.DIM_j):
if (i0-i)**2 + (j0-j)**2 > R**2:
kartta[i, j] = 'saari'
i0 = ly.DIM_i - R
j0 = ly.DIM_j - R
for i in range(i0-1, ly.DIM_i):
for j in range(j0-1, ly.DIM_j):
if (i0-i)**2 + (j0-j)**2 > R**2:
kartta[i, j] = 'saari'
i0 = ly.DIM_i - R
j0 = R
for i in range(i0-1, ly.DIM_i):
for j in range(0, j0+1):
if (i0-i)**2 + (j0-j)**2 > R**2:
kartta[i, j] = 'saari'
Kartta on taulukko, joka kertoo, onko ruutu maata, vettä vai rantaa.
ly.saaret on työkaluni tuottama lista saarien määrittelyistä: nimi, keskipiste, muoto ja asento
ly.saarella on työkaluni tuottama funktio, joka kertoo, onko ruutu saarta kuvaavan ellipsin sisällä.
def init_kartta():
kartta = np.full((ly.DIM_i, ly.DIM_j), 'jarvi', dtype='U5')
for saari in ly.saaret:
(name, (i0, j0), w, h, kulma) = saari
# skannataan varmuuden vuoksi koko järvi, vaikka riittäisi
# skannata suorakaide, jonka sisällä ellipsi on
for i in range(1, ly.DIM_i-1):
for j in range(1, ly.DIM_j-1):
if ly.saarella(i, j, i0, j0, w, h, kulma) <= 0:
kartta[i, j] = 'saari'
# leikataan 'piikit'
# Pienen ympyrän kylkeen saattaa jäädä yksittäinen ruutu
# markkeeraamaan pyöreyttä.
# (Yo. kommentti on vain tulevaisuuden minulle tiedoksi :-)
for i in range(1, ly.DIM_i-1):
for j in range(1, ly.DIM_j-1):
if kartta[i, j] == 'saari':
if kartta[i-1, j] == 'jarvi' and kartta[i+1, j] == 'jarvi':
kartta[i, j] = 'jarvi'
elif kartta[i, j-1] == 'jarvi' and kartta[i, j+1] == 'jarvi':
kartta[i, j] = 'jarvi'
# järven rannat merkataan maaksi, jotta saadaan
# reuna-ehdot toimimaan
kartta[0:ly.DIM_i, 0] = 'saari'
kartta[0:ly.DIM_i, 1] = 'saari'
kartta[0:ly.DIM_i, ly.DIM_j-1] = 'saari'
kartta[0:ly.DIM_i, ly.DIM_j-2] = 'saari'
kartta[0, 0:ly.DIM_j] = 'saari'
kartta[1, 0:ly.DIM_j] = 'saari'
kartta[ly.DIM_i-1, 0:ly.DIM_j] = 'saari'
kartta[ly.DIM_i-2, 0:ly.DIM_j] = 'saari'
# Ei tehdä suorakulmaista järveä.
# Pyöristetään nurkat.
kulmatf(kartta, 45)
# Merkitään karttaan rannat
reunapisteet(kartta)
return kartta
'''
Koska järven rannoilla pitää laskennassa ottaa huomioon reunaehdot,
merkitään rannat karttaan.
Jos ruutu on saarella, mutta jokin sen viereisistä ruuduista järvellä,
merkitään ruutu rannaksi.
'''
def reunapisteet(kartta):
for i in range(1, ly.DIM_i-1):
for j in range(1, ly.DIM_j-1):
if kartta[i, j] == 'saari':
rannallako(kartta, i, j)
def rannallako(kartta, i, j):
if kartta[i, j+1] == 'jarvi':
kartta[i, j] = 'ranta'
elif kartta[i, j-1] == 'jarvi':
kartta[i, j] = 'ranta'
elif kartta[i-1, j] == 'jarvi':
kartta[i, j] = 'ranta'
elif kartta[i+1, j] == 'jarvi':
kartta[i, j] = 'ranta'
Tätä ei ole helppo selittää.
Virtausten ja pinnankorkeuden muutokset riippuvat viereisten kuutioiden tilasta. Entä jos viereiden kuutio onkin maalla?
Hakukoneilemalla 'fluid mechanics boundary layer' löysin toinen toistaan matemaattisempia selityksiä, miten ottaa rannat huomioon. En jaksanut perehtyä, mutta pari huomiota jäi mieleeni.
Rannan tuntumaan voi ajatella vyöhykkeen, jossa vesi ei virtaa rannan suuntaisesti eikä järvelle tai sieltä rantaan päin. Oikeassa järvessä aallot loiskuvat rantaan, mutta keskimäärin vesi ei nouse eikä laske, eli ei ole nettovirtausta.
Sattui niin kivasti, että tämän ohjelmani aluksi nollaan taulukot, joissa ylläpidetään tietoa virtauksista, eikä taulukoita sen jälkeen päivitetä siltä osin kuin ruudut ovat maalla.
Paine — tässä tapauksessa pinnan korkeus — on kiperämpi juttu. Kirjaviisauksien mukaan paine-eron kapean rantavyöhykkeen yli pitäisi olla nolla. Loogista. Yhtälöt eivät erota maata vedestä, mutta ymmärtävät, että kun paine rajan kahden puolen on sama, ei siitä mennä yli. Eli siis paine nollaksi, eli pinnankorkeudet samoiksi. Samoiksi missä? Välille 'ranta' — 'saari'
 Rantavyöhyke. Lila on vettä, oranssi saaren rantaa,
jonne kopion pinnankorkeuden arvot.
Rantavyöhyke. Lila on vettä, oranssi saaren rantaa,
jonne kopion pinnankorkeuden arvot.
Homma hoituu vaikkapa kopioimalla pinnankorkeuden arvot rantavyöhykkeeltä ruudun verran 'sisämaahan'. Paitsi kuvan ongelmaa: Samaan rutuun pitäisi saada kaksi eri pinnankorkeuden arvoa.
Minulla on ollut monta loistavaa ideaa, miten ratkaista yo. ongelma ja samalla sekunnilla, kun olen idean saanut, olen alkanut sitä myös ohjelmoida.
Mikään kuningasajatuksistani ei ole tuottanut kunnollista lopputulosta ja tuloksen nähtyäni minun oli helppo ymmärtää, miksei idea ollutkaan kovin hyvä. Hetken harkinta olisi pelastanut paljolta turhalta työltä.
Yksi ideoistani oli kirjoittaa alusta saakka erikseen yhtälöt rantavyöhykkeelle. Sekin tuotti 'seisovia aaltoja' laajalle alueelle. Ehkä rosoreunainen ranta tuottaa oikeasti tuollaisen ilmiön. Onneksi näin taidetta tehdessä tuo ei haittaa.

Seuraavat kolme funktiota kopioivat kuvan lilalta vyöhykkeeltä pinnankorkeuden arvoja oranssille vyöhykkeelle.
def rantavedet(kartta):
rannat = []
for i in range(1, ly.DIM_i-1):
for j in range(1, ly.DIM_j-1):
if kartta[i, j] == 'ranta':
viereiset = []
# for (m, n) in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]:
for m in range(i-1, i+2):
for n in range(j-1, j+2):
if kartta[m, n] == 'jarvi':
viereiset.append((m, n))
if len(viereiset) > 0:
rannat.append(((i, j), viereiset))
return rannat
def tasaa_paineita(rho, rannat):
for (p0, viereiset) in rannat:
rho[p0] = keskiarvo(p0, rho, viereiset)
def keskiarvo(p0, rho, viereiset):
N = float(len(viereiset))
if N > 0:
x = 0
for viereinen in viereiset:
x += rho[viereinen]
return x/N
else:
return rho[p0]
def test_kartta():
tmp = np.full((ly.DIM_i, ly.DIM_j), -1.0)
kartta = init_kartta()
rannat = rantavedet(kartta)
for i in range(0, ly.DIM_i):
for j in range(0, ly.DIM_j):
if kartta[i, j] == 'jarvi':
tmp[i, j] = -2.0
elif kartta[i, j] == 'ranta':
tmp[i, j] = 1.0
elif kartta[i, j] == 'saari':
tmp[i, j] = 2.0
for (po, viereiset) in rannat:
for p1 in viereiset:
tmp[p1] = -1.0
test_plt1(tmp, 'rannat')
return tmp
Luodaan taulukko väriaineille
Jos parametri maasto=True, maat ja vedet peitetään alussa satunnaisesti levitetyillä väriaineilla.
Toinen vaihtoehto on roiskia simuloinnin alussa maisemaan pieniä yksittäisiä väriläiskiä alempana olevalla funktiolla.
def init_paint(paint):
# paint = np.full((ly.DIM_i, ly.DIM_j), 0.0)
# if kwargs['maasto']:
tau = 0.97
pnt0 = par.pnt_0
paint[0, 0] = 0.0 # random.uniform(-pnt0, pnt0)
for i in range(1, ly.DIM_i):
paint[i, 0] = tau*paint[i-1, 0] + \
(1.0-tau)*random.uniform(-pnt0, pnt0)
for j in range(1, ly.DIM_j):
paint[0, j] = tau*paint[0, j-1] + \
(1.0-tau)*random.uniform(-pnt0, pnt0)
for i in range(1, ly.DIM_i):
for j in range(1, ly.DIM_j):
x = tau*paint[i-1, j] + (1.0-tau)*random.uniform(-pnt0, pnt0)
y = tau*paint[i, j-1] + (1.0-tau)*random.uniform(-pnt0, pnt0)
# paint[i, j] = min(par.pnt_cut, max(-par.pnt_cut, (x+y)/2.0))
paint[i, j] = (x+y)/2.0
print('paint min max: ', np.min(paint), np.max(paint))
return paint # np.where(abs(paint) < 0.02*par.pnt_0, 0, paint)
# def init_paint(kartta, **kwargs):
# paint = np.full((ly.DIM_i, ly.DIM_j), 0.0)
# if kwargs['maasto']:
# tau = 0.97
# pnt0 = par.pnt_0
# paint[0, 0] = 0.0 # random.uniform(-pnt0, pnt0)
# for i in range(1, ly.DIM_i):
# paint[i, 0] = tau*paint[i-1, 0] + \
# (1.0-tau)*random.uniform(-pnt0, pnt0)
# for j in range(1, ly.DIM_j):
# paint[0, j] = tau*paint[0, j-1] + \
# (1.0-tau)*random.uniform(-pnt0, pnt0)
# for i in range(1, ly.DIM_i):
# for j in range(1, ly.DIM_j):
# x = tau*paint[i-1, j] + (1.0-tau)*random.uniform(-pnt0, pnt0)
# y = tau*paint[i, j-1] + (1.0-tau)*random.uniform(-pnt0, pnt0)
# # paint[i, j] = min(par.pnt_cut, max(-par.pnt_cut, (x+y)/2.0))
# paint[i, j] = (x+y)/2.0
# print('paint min max: ', np.min(paint), np.max(paint))
# return paint # np.where(abs(paint) < 0.02*par.pnt_0, 0, paint)
Roiskaistaan maisemaan muutama väritäplä. Väritäplän muotoilun pitäisi onnistua parilla sisäkkäisellä for-silmukalla, mutta sitä oli yllättävän vaikea suunnitella, joten hätäpäissäni turvauduin copy-pasteamiseen.
Tämän ohjelman alussa esitellyn maalari-olion toivomuksesta tehdään jokaista punaista roisketta vastaava sininen. Näin värien keskiarvo pysyy nollana, mikä helpottaa maalarin työtä.
Maalari-olio maalaa positiiviset arvot punaisen sävyillä ja negatiiviset sinisen sävyillä, joten ohjelmassa riittää tarkastella vain yhden väriaineen liikkeitä. Sekoittuessaan väriaineet neutraloivat toisensa, koska maalari maalaa nollaruudut valkoisella.
def roiskeita(paint):
for k in range(0, 50):
clr = random.uniform(0, par.pnt_0)
ip = random.randrange(2, ly.DIM_i-3)
jp = random.randrange(2, ly.DIM_j-3)
paint[ip, jp] = clr
paint[ip-1, jp] = 2.0/3.0*clr
paint[ip+1, jp] = 2.0/3.0*clr
paint[ip-2, jp] = 1.0/3.0*clr
paint[ip+2, jp] = 1.0/3.0*clr
paint[ip, jp-1] = 2.0/3.0*clr
paint[ip, jp+1] = 2.0/3.0*clr
paint[ip, jp-2] = 1.0/3.0*clr
paint[ip, jp+2] = 1.0/3.0*clr
paint[ip-1, jp-1] = 0.5*clr
paint[ip-1, jp+1] = 0.5*clr
paint[ip+1, jp-1] = 0.5*clr
paint[ip+1, jp+1] = 0.5*clr
clr = -clr
ip = random.randrange(2, ly.DIM_i-3)
jp = random.randrange(2, ly.DIM_j-3)
paint[ip, jp] = clr
paint[ip-1, jp] = 2.0/3.0*clr
paint[ip+1, jp] = 2.0/3.0*clr
paint[ip-2, jp] = 1.0/3.0*clr
paint[ip+2, jp] = 1.0/3.0*clr
paint[ip, jp-1] = 2.0/3.0*clr
paint[ip, jp+1] = 2.0/3.0*clr
paint[ip, jp-2] = 1.0/3.0*clr
paint[ip, jp+2] = 1.0/3.0*clr
paint[ip-1, jp-1] = 0.5*clr
paint[ip-1, jp+1] = 0.5*clr
paint[ip+1, jp-1] = 0.5*clr
paint[ip+1, jp+1] = 0.5*clr
return(paint)
# Ihan vaan muistutus siitä, mitä kaikkea numpy:llä voi tehdä
# kätevän tehokkaasti
# def nollaa_vari_huiput(a):
# return np.where(abs(a) < 0.99*par.pnt_0, a, 0)
def test_plots():
x = np.full(ly.DIM_j, 0.0)
y = np.full(ly.DIM_i, 0.0)
for j in range(0, ly.DIM_j):
x[j] = par.ds*j
for i in range(0, ly.DIM_i):
y[i] = par.ds*i
test_kartta()
# test_reunat()
test_kosket()
# test_valuma(x, y)
##############################################################
# Pääohjelman alku
##############################################################
def main():
print(tim.datetime.now())
random.seed()
# Turha jatkaa simulointia numpy-rutiinien ylivuodon jälkeen
# Asetetaan ylivuoto virhetilanteeksi
np.seterr(over='raise')
plt.matplotlib.use('qtagg')
plt.ioff()
rho = np.full((ly.DIM_i, ly.DIM_j), par.rho_0)
Dt0_rho = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt1_rho = np.full((ly.DIM_i, ly.DIM_j), 0.0)
rho_nxt = np.full((ly.DIM_i, ly.DIM_j), par.rho_0)
u = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt0_u = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt1_u = np.full((ly.DIM_i, ly.DIM_j), 0.0)
u_nxt = np.full((ly.DIM_i, ly.DIM_j), 0.0)
v = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt0_v = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt1_v = np.full((ly.DIM_i, ly.DIM_j), 0.0)
v_nxt = np.full((ly.DIM_i, ly.DIM_j), 0.0)
paint = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt0_paint = np.full((ly.DIM_i, ly.DIM_j), 0.0)
Dt1_paint = np.full((ly.DIM_i, ly.DIM_j), 0.0)
paint_nxt = np.full((ly.DIM_i, ly.DIM_j), 0.0)
kartta = init_kartta()
rannat = rantavedet(kartta)
if par.maasto:
paint = init_paint(paint)
else:
paint = roiskeita(paint)
Fe_u, Fe_v = kosket(vastapyorre=True)
# Luodaan maalarin työpaja
Maalari = Cl_Maalari(paint)
# Tein toisenkin maalailemaan zoomauksia, mutta kaksi maalaria
# vilkuttelivat kilvan tuotoksiaan niin ikävästi, että
# jouduin kommentoimaan toisen sivuun.
# zoom = Cl_Maalari()
n = 0
t = 0.0
dt = par.dt
overflow = False
# +++++++++++++++ simulointi ++++++++++++++++++++++++++
Muuntaessani x- ja y- suunnan osittaisdifferentiaaliyhtälöitä differenssiyhtälöiksi, olisin voinut muuntaa myös aikaderivaatat differenssiyhtälöiksi ja sen jälkeen ratkaista nopeuksien, pinnankorkeuden ja väriaineiden konsentraatiot kussakin ruudussa hetkellä t + dt niiden arvojen hetkellä t perusteella. Menettelyä kutsutaan eulerin algoritmiksi.
Sitä aluksia kokeilinkin. Tiesin, että Eulerin algoritmi ei ole kovin tarkka, mutta ajattelin, ettei se haittaa näin taiteen teossa. Eri juttu, jos suunnittelisin lentokoneita. (Tosin Boeing 737 MAX onnettomuuksien syistä päätellen, eivät lentokoneiden suunnittelijatkaan ole turhan tarkkoja).
Pieni virhe ei olisi minua haitannut, mutta virhettä kertyi niin, että tietokoneestani 'loppuivat numerot' — Järven pintaan pullahti niin korkea kupru, ettei tietokoneestani löytynyt riittävän suurta numeroa siitä kertomaan. Tapahtui 'floating point overflow', kuten tietokonekielellä on tapana sanoa.
Onneksi wikipedia tiesi kertoa Heunin menetelmästä
while t < par.tf and not overflow:
# simuloinnin alkuaskelilla roiskitaan väritäpliä maisemaan
if n < 100 and not par.maasto:
paint = roiskeita(paint)
# try — except rakentaan avulla pysäytän simuloinnin, jos
# tulee 'floating point overflow'
try:
# Lasketaan kussakin ruudussa aikaderivaatat nopeudella
# ja pinnankorkeudelle: Heun vaihe 1
df.dfdt(kartta, rho, u, v, paint, Fe_u, Fe_v,
Dt0_rho, Dt0_u, Dt0_v, Dt0_paint)
rho_nxt = rho + Dt0_rho*dt
paint_nxt = paint + Dt0_paint*dt
u_nxt = u + Dt0_u*dt
v_nxt = v + Dt0_v*dt
# Heunin menetelmän vaihe 2.
df.dfdt(kartta, rho_nxt, u_nxt, v_nxt, paint_nxt, Fe_u, Fe_v,
Dt1_rho, Dt1_u, Dt1_v, Dt1_paint)
rho_nxt = rho + (Dt0_rho + Dt1_rho)/2.0*dt
paint_nxt = paint + (Dt0_paint + Dt1_paint)/2.0*dt
u_nxt = u + (Dt0_u + Dt1_u)/2.0*dt
v_nxt = v + (Dt0_v + Dt1_v)/2.0*dt
except FloatingPointError as err:
print('Overflow ', err)
print('n, t ', n, t)
overflow = True
# Tämä näyttänee hämärältä?
# Vaihdetaan 'vanhoihin' ja 'uusiin' taulukoihin osoittavat
# pointterit.
# Useimmat muuttujat tässä simuloinnissa ovat isoja numpy —
# 'numeric python' — taulukoita, joita pitää käsitellä harkiten
rho, rho_nxt = rho_nxt, rho
paint, paint_nxt = paint_nxt, paint
u, u_nxt = u_nxt, u
v, v_nxt = v_nxt, v
Maalari.sys_plot(rho, u, v, paint, n)
tasaa_paineita(rho, rannat)
# i0 = 145
# i1 = 185
# j0 = 90
# j1 = 135
# zoom.sys_plot(rho[i0:i1, j0:j1], u[i0:i1, j0:j1], v[i0:i1, j0:j1],
# paint[i0:i1, j0:j1], n)
t += dt
n += 1
print(n, t)
plt.close('all')
print('Valmis! ', n, t, tim.datetime.now())
if __name__ == "__main__":
main()